Hi - I’d like to understand the loads that OpenFAST outputs a little bit better. I’m interested in the outputs of simulations with a fixed foundation (monopile or jacket) - I use SubDyn below the interface and ElastoDyn above. I find that the ElastoDyn tower base loads (TwrBs…) match the SubDyn interface loads (Intf…) and that these loads are different to the SubDyn elastic loads (MaBn[F|M]K…) in the element at the end connected to the interface node. Moreover, I can broadly recover the SubDyn interface loads by resolving the SubDyn elastic loads (MaBn[F|M]K…) in the element at the end connected to the interface node and adding the inertial load associated with the Guyan (interface DOFs) when the number of CB modes is 0 - consistent with the SubDyn interface and ElastoDyn tower base loads being reactions. Tower strain gauges similarly appear to be internal reactions, not necessarily internal strain i.e. M=EI * curvature? Perhaps I’m mistaken. Based on other threads, like Mlife and Fatigue - Wind & Water / Computer-Aided Engineering Software Tools - NREL Forum, it seems as if it’s common to use the ElastoDyn tower loads to derive stresses and calculate lifes etc - is this appropriate? I’d have thought we’d evaluate life using internal strain loads (SubDyn-like elastic) loads rather than reactions. Thanks! @Jason.Jonkman any thoughts?
Dear @Sam.Ramsahoye,
I’m not sure I fully understand your question. I’ll just clarify that in ElastoDyn, the tower-base reaction loads are the loads transmitted to the platform through the tower. The SubDyn member-level loads include only the elastic contribution or inertial contribution to this reaction load. The difference can be explained through a simple linear mass (m), spring (k), damper (c) system cantilevered with applied force (F), with equation of motion (in terms of displacement of the mass, q):
m * qdd + c * qd + k * q = F
where d represents the first time derivative.
The force transmitted from the mass to the base is Fr = c * qd + k q, which is equivalent to Fr = F - m * qdd through equations of motion.
ElastoDyn will compute the latter (Fr = F - m * qdd). The member-level load in SubDyn will only output the elastic contribution (k * q) or the inertial contribution (m * qdd).
I hope that helps.
Best regards,
Dear @Jason.Jonkman ,
Thanks very much for your response and apologies that my original question wasn’t very clear - OpenFAST’s behaviour is clear to me now.
I’m curious, why does the standard appear to be to report Fr = F - m qdd = c qd + k q? My recollection is that Bladed does something very similar. It’s true that this is the load applied to a section but the actual strain in the section is given only by the kq term. In this sense, I find the use of the term strain gauge in referring to F_r type loads to be confusing. There will be times when only the k*q component will be of interest such as when assessing material yielding / fatigue.
When OEMs report turbine interface loads, do you know if the standard is to report reactions (c qd + k q = F - m qdd) or elastic loads (kq)?
Thanks very much for your help!
Best wishes,
Sam
Dear @Sam.Ramsahoye,
I would say that the total load transferred through the member is Fr = c * qd + k q = F - m * qdd is the correct load to output for calculating stress.
The elastic contribution (k * q) is often quite a bit higher than the damping contribution (c * qd), and so, is often a reasonable approximation of Fr. Note that in some cases, such as when damping is defined at the system level (modal damping) rather than at the component level, it is impossible to know the damping contribution at the component level (as is the case in SubDyn), which is why this term is often neglected in the reaction load output.
Also note that the inertial contribution (m * qdd ) is often interesting to quantify, but it is typically not a good approximation of Fr.
FYI: The ElastoDyn calculation of Fr = F - m * qdd is preferred over Fr = c * qd + k q because the former works whether the member (blade, tower) is modeled rigidly or flexibly, whereas the latter only works when flexible.
Best regards,
Dear Jason and all,
I am aware that the academic model of the NREL 5MW wind turbine is not optimized for any specific IEC class (as also stated in Post 5718). However, I am currently conducting analysis for IEC Class 1A, and in order to evaluate the potential of our Flywheel (FW) system in reducing tower loads and extending fatigue life, it is necessary to first define the baseline fatigue life of the original model.
My calculation approach follows these steps:
-
Use the sectional dimensions of the NREL 5MW tower (diameter and wall thickness).
-
Generate S-N curves for welded tubular sections according to DNV guidelines.
-
Simulate and extract Rainflow Counting (RFC) data for fatigue analysis.
-
Apply Miner’s rule using RFC and S-N curves.
-
Calculate damage and derive the corresponding fatigue life.
I performed this analysis for:
-
Tower base (assumed as Tower Node 1),
-
Tower nodes 2 to 10, since Tower model conatins 11 nodes and outputs are restricted to 9 nodes (excluding the base and top),
-
Yaw bearing (assumed as Tower Node 11).
Since fatigue in the tower is most critical in the fore-aft direction (at least from my simulations), I used RFC data for the Myt moment at the base and along the tower. For the tower top (yaw bearing), I used Myp (non-rotating system) since Myt is not directly available there.
The fatigue life trend across the tower base and sections (all using the yt-axis) is consistent, while the yaw bearing (using the yp-axis) shows a significantly different trend.
Q1: Could this discrepancy be due to differences in the coordinate systems?
Q2: Is there any other recommended approach to estimate fatigue life at the tower top without changing the output nodes from 3 to 11 and repeating all simulations?
Thank you in advance for your insights.
Best regards,
Abhinay Goga
Dear @Abhinay.Goga,
Overall your approach sounds correct. Just a few comments:
- Along the tower, the tower-bending fore-aft bending moment is expressed in the local tower coordinate system (Lyt), which matches the local deflection of the tower, so, this should be close to the tower-base coordinate system (yt) at the tower base, as well as close to the tower-top/platform coordinate system (yp) at the tower top.
- A tower with
TwrNodes= 11 elements will have 11 internal nodes (because ElastoDyn uses nodes located within the centers of equal-length elements), plus the base and top nodes (13 nodes total in your case). So, by outputting nodes 2-10 will result in a bit wider distance between the base and node 2 and the top and node 10 compared to the spacing between the internal nodes. - The tower diameter and thickness of the NREL 5-MW baseline turbine vary linearly along the tower, so, I would overall expect a smooth curve and I’m not sure why you are seeing a jump between nodes 10 and the top. Have you verified that the diameter and thickness you are using are also linear along the tower?
Best regards,
Dear Jason and all,
Thank you for confirming the coordinate systems.
Thank you for the clarification on how ElastoDyn handles the TwrNodes setting.
Just to confirm: if the ElastoDyn_Tower file contains 11 nodes, I initially assumed that assigning all 11 nodes to TwrNodes in ElastoDyn would result in 10 tower sections, and that the nodal outputs (from 2 to 10) would correspond to the connecting points between these sections.
However, based on your explanation, this assignment actually creates 11 elements, meaning 11 tower sections, rather than 10 as defined in the tower input file. And further, ElastoDyn produces outputs at the center of each element, not at the node locations (i.e., not at the connecting points between elements).
Could you kindly confirm if this understanding is correct?
| Height | Diameter | Wall Thickness |
|---|---|---|
| m | m | m |
| 0.00 | 6.000 | 0.03510 |
| 8.76 | 5.787 | 0.03406 |
| 17.52 | 5.574 | 0.03302 |
| 26.28 | 5.361 | 0.03198 |
| 35.04 | 5.148 | 0.03094 |
| 43.80 | 4.935 | 0.02990 |
| 52.56 | 4.722 | 0.02886 |
| 61.32 | 4.509 | 0.02782 |
| 70.08 | 4.296 | 0.02678 |
| 78.84 | 4.083 | 0.02574 |
| 87.60 | 3.870 | 0.02470 |
As shown in the table, the tower outer diameter and wall thickness values are linearly interpolated. I have also included the 30% increase in wall thickness as described in the NREL TP-500-38060 report. To verify the accuracy, I calculated the mass of each tower section by determining the volume and multiplying it with a density of 8500 kg/m³ (to account for paint, bolts, welds, and flanges). The overall tower mass is within a 0.02% error margin, confirming the reliability of the interpolation.
As you mentioned, I also expected to observe a consistent trend in fatigue life along the tower.
Regards,
Abhinay Goga
Dear @Abhinay.Goga,
I believe I understand the issue now. The tower stations defined in the ElastoDyn tower file do not need to align with the tower analysis nodes of ElastoDyn. The number of tower elements (of equal length) and tower analysis nodes (located in the centers of the equal length elements) are defined in the ElastoDyn primary input file by TwrNodes. The number of tower stations (NTwInpSt) and the cross-section mass and stiffness at those stations is defined in the ElastoDyn tower file. If the stations don’t align with the locations of the tower analysis nodes, ElastoDyn wil linearly l interpolate the data from the stations to the analysis nodes. In your case, I suspect you’ve set NTwInpSt = 11 while using TwrNodes = 20 (which is how NREL provided this OpenFAST model). So, you actually have 20 nodes and are only outputting nodes 2-10 from these.
Best regards,
Dear Jason and all,
In my current setup, both NTwInpSt and TwrNodes are set to 11.
My current approach: I treat the outputs from node 2 to 10 as representative of the connecting tower sections.
| Height (m) | Height Fraction | Tower File Nodes | ElastoDyn Nodes | ElastoDyn Outputs | Plot Nodes | Distance between nodes (m) |
|---|---|---|---|---|---|---|
| 0.00 | 0.00 | 0 | 1 | None | Tower Base | |
| 8.76 | 0.10 | 1 | 2 | 2 | 1 | 8.76 |
| 17.52 | 0.20 | 2 | 3 | 3 | 2 | 8.76 |
| 26.28 | 0.30 | 3 | 4 | 4 | 3 | 8.76 |
| 35.04 | 0.40 | 4 | 5 | 5 | 4 | 8.76 |
| 43.80 | 0.50 | 5 | 6 | 6 | 5 | 8.76 |
| 52.56 | 0.60 | 6 | 7 | 7 | 6 | 8.76 |
| 61.32 | 0.70 | 7 | 8 | 8 | 7 | 8.76 |
| 70.08 | 0.80 | 8 | 9 | 9 | 8 | 8.76 |
| 78.84 | 0.90 | 9 | 10 | 10 | 9 | 8.76 |
| 87.60 | 1.00 | 10 | 11 | None | Yaw bearing | 8.76 |
Based on your comments:
| Height (m) | Height Fraction | ElastoDyn Nodes | Plot Nodes | Distance between nodes (m) |
|---|---|---|---|---|
| 0 | 0.000 | 1 | Tower Base | |
| 7.3 | 0.083 | 2 | 1 | |
| 14.6 | 0.167 | 3 | 2 | 10.95 |
| 21.9 | 0.250 | 4 | 3 | 3.65 |
| 29.2 | 0.333 | 5 | 4 | 3.65 |
| 36.5 | 0.417 | 6 | 5 | 3.65 |
| 43.8 | 0.500 | 7 | 6 | 3.65 |
| 51.1 | 0.583 | 8 | 7 | 3.65 |
| 58.4 | 0.667 | 9 | 8 | 3.65 |
| 65.7 | 0.750 | 10 | 9 | 3.65 |
| 73 | 0.833 | 11 | 10 | 3.65 |
| 80.3 | 0.917 | 12 | 11 | |
| 87.6 | 1.000 | 13 | Yaw bearing | 10.95 |
I now assume that this might be the reason for the deviation I observe in the fatigue life trend plots. Due to the spatial mismatch between how the nodes are defined in the ElastoDyn_Tower file and how the outputs are generated (i.e., outputs being taken at the center of elements rather than at nodal connection points), this could lead to an apparent discontinuity in the fatigue results near base and tower top.
Could you please confirm whether this is the correct interpretation?
Regards,
Abhinay Goga
Dear @Abhinay.Goga,
Because you’ve set TwrNodes = 11, that means each element is 87.6/11 = 7.964 m long and the 1st node, being at the center of the first element is at an elevation of 3.982, node 2 is at 11.945 m, etc. The internal analysis nodes are numbered 1 to TwrNodes and the tower-base node is numbered 0 (output through TwrBsMyt) and the tower-top node (output through YawBrMyp) is numbered TwrNodes+1 = 12 in your case.
Best regards,
Dear Jason and all,
Considering your insights, I have identified issues with the tower section diameters and thicknesses I previously used.
Initially, I had assumed a constant spacing of 8.76 m for each tower section. However, I have now realized that the ElastoDyn output nodes 2 to 10 are positioned at the following heights (in meters):
[11.945, 19.909, 27.872, 35.836, 43.800, 51.763, 59.727, 67.690, 75.654], with the base at 0 m and the tower top at 87.6 m.
Using the same linear interpolation strategy, I have now extracted the corresponding diameter and thickness values at these ElastoDyn output nodes. For the fatigue analysis, I am assuming that tower sections are butt welded to each other, and I am neglecting flange bolt design S-N curves.
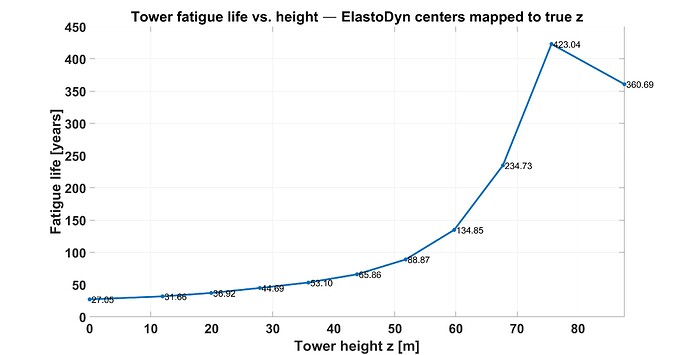
After adjusting the section lengths, diameters, and thicknesses based on the correct node positions, the fatigue life curve now shows a smooth trend up to node 10. However, at the top sections, particularly at the yaw bearing, there is a noticeable drop in fatigue life.
From the calculated DELs, I observe a continuous reduction in fatigue from base to top for Wöhler slopes of 3 to 5. Here the results fro slope 3:
| TwrBsFxt (kN) | TwrBsFyt (kN) | TwrBsFzt (kN) | TwrBsMxt (kN-m) | TwrBsMyt (kN-m) | TwrBsMzt (kN-m) |
|---|---|---|---|---|---|
| 897.40 | 473.35 | 234.59 | 34641.45 | 57360.39 | 11275.26 |
| TwHt1FLxt (kN) | TwHt1FLyt (kN) | TwHt1FLzt (kN) | TwHt1MLxt (kN-m) | TwHt1MLyt (kN-m) | TwHt1MLzt (kN-m) |
| 893.43 | 473.20 | 234.43 | 29365.44 | 47938.38 | 11275.62 |
| TwHt2FLxt (kN) | TwHt2FLyt (kN) | TwHt2FLzt (kN) | TwHt2MLxt (kN-m) | TwHt2MLyt (kN-m) | TwHt2MLzt (kN-m) |
| 870.57 | 465.28 | 234.34 | 25932.36 | 41916.79 | 11275.71 |
| TwHt3FLxt (kN) | TwHt3FLyt (kN) | TwHt3FLzt (kN) | TwHt3MLxt (kN-m) | TwHt3MLyt (kN-m) | TwHt3MLzt (kN-m) |
| 826.63 | 449.69 | 234.27 | 22615.08 | 36297.04 | 11275.65 |
| TwHt4FLxt (kN) | TwHt4FLyt (kN) | TwHt4FLzt (kN) | TwHt4MLxt (kN-m) | TwHt4MLyt (kN-m) | TwHt4MLzt (kN-m) |
| 768.34 | 428.56 | 234.25 | 19613.31 | 31628.35 | 11277.53 |
| TwHt5FLxt (kN) | TwHt5FLyt (kN) | TwHt5FLzt (kN) | TwHt5MLxt (kN-m) | TwHt5MLyt (kN-m) | TwHt5MLzt (kN-m) |
| 708.06 | 406.49 | 234.18 | 16676.22 | 27347.05 | 11275.38 |
| TwHt6FLxt (kN) | TwHt6FLyt (kN) | TwHt6FLzt (kN) | TwHt6MLxt (kN-m) | TwHt6MLyt (kN-m) | TwHt6MLzt (kN-m) |
| 656.55 | 386.90 | 234.17 | 13779.65 | 23195.29 | 11277.25 |
| TwHt7FLxt (kN) | TwHt7FLyt (kN) | TwHt7FLzt (kN) | TwHt7MLxt (kN-m) | TwHt7MLyt (kN-m) | TwHt7MLzt (kN-m) |
| 631.85 | 374.83 | 234.19 | 10888.98 | 19212.78 | 11277.22 |
| TwHt8FLxt (kN) | TwHt8FLyt (kN) | TwHt8FLzt (kN) | TwHt8MLxt (kN-m) | TwHt8MLyt (kN-m) | TwHt8MLzt (kN-m) |
| 633.91 | 369.47 | 234.19 | 8058.85 | 15484.41 | 11277.23 |
| TwHt9FLxt (kN) | TwHt9FLyt (kN) | TwHt9FLzt (kN) | TwHt9MLxt (kN-m) | TwHt9MLyt (kN-m) | TwHt9MLzt (kN-m) |
| 636.22 | 362.81 | 234.23 | 5344.91 | 12411.31 | 11275.28 |
| YawBrFxp (kN) | YawBrFyp (kN) | YawBrFzp (kN) | YawBrMxp (kN-m) | YawBrMyp (kN-m) | YawBrMzp (kN-m) |
| 618.80 | 343.24 | 234.28 | 2576.58 | 10823.01 | 11275.13 |
Any insights you might have to guide me understand and interpret this discontinuity in fatigue life at tower top would be greatly appreciated.
Regards,
Abhinay Goga
Dear @Abhinay.Goga,
I’m not sure. Regarding your DELs, I do see a change in curvature between output node 9 (analysis node 10) and the yaw bearing for the shear force along x. Perhaps that is the problem?
Best regards,
Dear Jason and all,
I am using the original tower file and the mode-shape coefficients exactly as provided in the regression folders. With a simple MATLAB script (below), I reconstruct the fore–aft mode shapes and then obtain the curvature and shear by taking the second and third derivatives, respectively.
FA1 = [0 0.7004 2.1963 -5.6202 6.2275 -2.504];
FA2 = [0 -70.5319 -63.7623 289.737 -176.513 22.0706];
phiPoly = @(a,x) x.^2 .* (a(2) + a(3)*x + a(4)*x.^2 + a(5)*x.^3 + a(6)*x.^4);
d1 = @(f,x) gradient(f,x);
d2 = @(f,x) gradient(d1(f,x),x); % curvature ~ \phi''
d3 = @(f,x) gradient(d2(f,x),x); % “shear” ~ \phi'''
x = linspace(0,1,600).';
PHI_FA1 = phiPoly(FA1,x); C_FA1 = d2(PHI_FA1,x); S_FA1 = d3(PHI_FA1,x);
PHI_FA2 = phiPoly(FA2,x); C_FA2 = d2(PHI_FA2,x); S_FA2 = d3(PHI_FA2,x);
figure('Name','Mode shapes & derivatives (FA)');
tiledlayout(3,2,'Padding','compact','TileSpacing','compact');
nexttile; plot(x,PHI_FA1,'-','LineWidth',1.5); grid on; title('Mode 1 shape \phi_1(x)'); ylabel('\phi');
nexttile; plot(x,PHI_FA2,'-','LineWidth',1.5); grid on; title('Mode 2 shape \phi_2(x)'); ylabel('\phi');
nexttile; plot(x,C_FA1,'-','LineWidth',1.5); grid on; title('Mode 1 curvature \phi'''''); ylabel('\phi''''');
nexttile; plot(x,C_FA2,'-','LineWidth',1.5); grid on; title('Mode 2 curvature \phi'''''); ylabel('\phi''''');
nexttile; plot(x,S_FA1,'-','LineWidth',1.5); grid on; title('Mode 1 shear \phi'''''''); xlabel('x=z/L'); ylabel('\phi''''''');
nexttile; plot(x,S_FA2,'-','LineWidth',1.5); grid on; title('Mode 2 shear \phi'''''''); xlabel('x=z/L'); ylabel('\phi''''''');
fprintf('\nTop BC checks (should be ~0):\n');
fprintf('phi''''(1): M1=%.2e, M2=%.2e | phi''''''(1): M1=%.2e, M2=%.2e\n', C_FA1(end), C_FA2(end), S_FA1(end), S_FA2(end));
From these plots, I observe a deviation in the third derivative (the “shear”-like quantity, ϕ′′′) starting at approximately 80% of the tower height. Is this the effect you were referring to?
Regards,
Abhinay Goga
Dear @Abhinay.Goga,
I was referring to the change in curvature in the figure you shared on October 15, whereby the curvature changes between output node 9 (analysis node 10) and the yaw bearing for the shear force along x.
Regarding your mode shape derivative plots, I’m guessing the numerical gradient computed by MATLAB is not accurate enough. That said, it is easy to compute the analytical derivative of a polynomial, e.g., for f(x) = a2 * x^2, df/dx = 2 * a2 * x and df^2/dx^2 = 2 * a2.
Best regards,
Dear Jason and all,
Thank you for the clarification regarding the curvature change near the tower top and your remarks. The DEL variations in shear/curvature are consistent with the observed fatigue-life trend. Since DELs are derived from RFC and I use them to compute fatigue life, the similarity between the DEL and fatigue-life curves is expected.
1. My current issue is why the yaw-bearing result does not follow the same trend as the tower-section results and shows a sudden variation. Is this discrepancy known, or is it more likely due to my post-processing (fatigue calculation and/or interpretation)?
2. To investigate the “shear proxy,” I switched to analytical derivatives of the fore-aft mode shapes and reproduced the curvature ϕ′′ and third derivative ϕ′′′ using the script below .
clear; clc;
FA1 = [0 0.7004 2.1963 -5.6202 6.2275 -2.504 ];
FA2 = [0 -70.5319 -63.7623 289.737 -176.513 22.0706 ];
% Helper to unpack a = [~,a2..a6]
getA = @(a) deal(a(2),a(3),a(4),a(5),a(6));
% Analytical evaluators for phi, phi'', phi'''
phi_anal = @(a,x) ...
(x.^2) .* (a(2) + a(3)*x + a(4)*x.^2 + a(5)*x.^3 + a(6)*x.^4);
phi2_anal = @(a,x) ...
( 2*(a(2) + a(3)*x + a(4)*x.^2 + a(5)*x.^3 + a(6)*x.^4) ) + ...
( 4*x .* (a(3) + 2*a(4)*x + 3*a(5)*x.^2 + 4*a(6)*x.^3) ) + ...
( x.^2 .* (2*a(4) + 6*a(5)*x + 12*a(6)*x.^2) );
phi3_anal = @(a,x) ...
( 6*(a(3) + 2*a(4)*x + 3*a(5)*x.^2 + 4*a(6)*x.^3) ) + ...
( 6*x .* (2*a(4) + 6*a(5)*x + 12*a(6)*x.^2) ) + ...
( x.^2 .* (6*a(5) + 24*a(6)*x) );
% Tip BCs (closed form) for quick checks
phi2_tip = @(a) 2*a(2)+6*a(3)+12*a(4)+20*a(5)+30*a(6);
phi3_tip = @(a) 6*a(3)+24*a(4)+60*a(5)+120*a(6);
% Optional normalization check at x=1: phi(1) = 1 -> a2+...+a6 = 1
phi1_at1 = @(a) a(2)+a(3)+a(4)+a(5)+a(6);
% Evaluate
x = linspace(0,1,600).';
PHI1 = phi_anal(FA1,x); C1 = phi2_anal(FA1,x); S1 = phi3_anal(FA1,x);
PHI2 = phi_anal(FA2,x); C2 = phi2_anal(FA2,x); S2 = phi3_anal(FA2,x);
% Plots (same layout as before)
figure('Name','Mode shapes & analytical derivatives (FA)');
tiledlayout(3,2,'Padding','compact','TileSpacing','compact');
nexttile; plot(x,PHI1,'LineWidth',1.5); grid on; title('Mode 1 shape \phi_1(x)'); ylabel('\phi');
nexttile; plot(x,PHI2,'LineWidth',1.5); grid on; title('Mode 2 shape \phi_2(x)'); ylabel('\phi');
nexttile; plot(x,C1,'LineWidth',1.5); grid on; title('Mode 1 curvature \phi'''''); ylabel('\phi''''');
nexttile; plot(x,C2,'LineWidth',1.5); grid on; title('Mode 2 curvature \phi'''''); ylabel('\phi''''');
nexttile; plot(x,S1,'LineWidth',1.5); grid on; title('Mode 1 shear proxy \phi'''''''); xlabel('x=z/L'); ylabel('\phi''''''');
nexttile; plot(x,S2,'LineWidth',1.5); grid on; title('Mode 2 shear proxy \phi'''''''); xlabel('x=z/L'); ylabel('\phi''''''');
% Tip boundary-condition checks (exact)
fprintf('\nTip BC checks (should be ~0 for free end):\n');
fprintf(' phi''''(1): M1=% .3e, M2=% .3e\n', phi2_tip(FA1), phi2_tip(FA2));
fprintf(' phi''''''(1): M1=% .3e, M2=% .3e\n', phi3_tip(FA1), phi3_tip(FA2));
% Optional normalization
fprintf('\nNormalization check phi(1)=a2+...+a6 (often ~1 after scaling):\n');
fprintf(' phi(1): M1=% .6f, M2=% .6f\n', phi1_at1(FA1), phi1_at1(FA2));
With this, the mode shapes and their derivatives are like this:
Many thanks in advance.
Best regards,
Abhinay Goga
Dear @Abhinay.Goga,
I would not expect a step change in results between the yaw bearing and tower section below, but I’m not sure what is causing it. If you simply look at the OpenFAST outputs, e.g., mean and standard deviation of the loads at the yaw bearing and tower section below, do you also see the step change, or is the issue isolated to your DEL post-processing?
Best regards,
Dear Jason and all,
I appreciate your patience and continued support in this matter.
As shown below, for one particular simulation scenario, the mean and standard deviation (SD) of the fore-aft bending moment between the yaw bearing and the top tower node (node 9) are consistent with the overall trend—i.e., both values decrease progressively from the bottom to the top (between node 8 and node 9).
However, when I examine a shorter time window (for example, a 30-second snippet), this trend disappears, and I instead observe an increase in SD between node 9 and the yaw bearing.
In a realistic situation, even without active yaw control, I would expect some yaw degree of freedom (Yaw DOF), which is why I kept it enabled. Setting Yaw DOF = True allows relative load transfer between the rigid nacelle and the yaw bearing, which is also influenced by the YawSpring and YawDamp parameters.
After reviewing the discussion (Nacelle Yaw Parameter (YawSpr and YawDamp)), I am now considering whether disabling the Yaw DOF might help in diagnosing the cause of this discrepancy.
Would you recommend switching off the Yaw DOF for a diagnostic run?
Regards
Abhinay Goga
Dear @Abhinay.Goga,
Based on your statistical analysis of the 10-minute simulation and 30-s snapshot, I would guess the differing trend at 30 s is simply a matter of a lack of statistical convergence. Further, I would expect the DEL calculation is simply exaggerating this difference, so, perhaps your original issue is just a lack of statistical convergence.
I would not expect the YawDOF in ElastoDyn to influence the trend because you are outputting the yaw bearing loads in the tower-top coordinate system (p), which does not rotate about the yaw axis with the nacelle, and is consistent with the local tower coordinate system (Lt) you are using at the tower sections below. (That said, enabling/disabling YawDOF may generally effect the overall system response.)
Best regards,