WISDEM tower/monopile optimization: effect of different initial configurations on optimal solution

[Henny.Bottini]

Hello everybody,

I am optimizing the tower/monopile of a 20-MW offshore wind turbine with the following settings:
design variables: outer_diameter, layer_thickness (for both tower and monopile)
objective function: structural_mass
tower constraints: stress, global_buckling, shell_buckling, taper, slope, frequency_1 (lower_bound=0.05, upper_bound=0.3), thickness_slope
monopile constraints: stress, global_buckling, shell_buckling, taper, slope, frequency_1 (lower_bound=0.05, upper_bound=0.16), thickness_slope, pile_depth, tower_diameter_coupling
solver: SLSQP
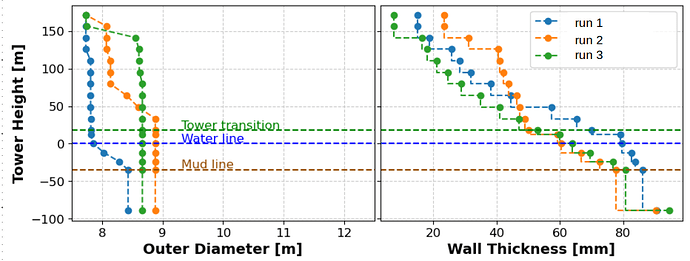
To explore the design space, I run three optimizations with the above settings but different initial configurations (that is, different initial distributions of outer diameters and layer thickness):
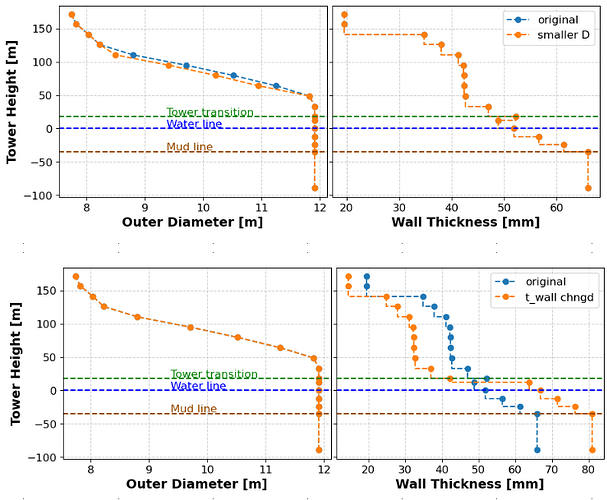
run 1: original configuration (plot label= original)
run 2: tower diameter reduced by 0.3 m at four points; layer thickness distribution original (plot label= smaller D)
run 3: wall thickness reduced by 10 mm all along the tower and increased by 15 mm all along the monopile; tower and monopile diameter distributions original (plot label = t_wall chngd)
See the plots below.

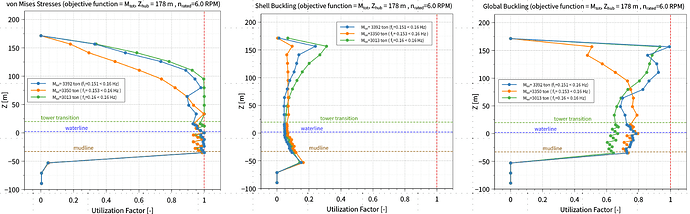
The three optimizations are successful. I can also verify that the constraints are respected by looking at these plots of the utilization factors for the von Mises stress, shell buckling, and global buckling (run 1: cyan, run 2: orange, run 3: green):

and the values of the 1st natural frequency of the monopile optimal designs are:
run 1: 0.151 Hz < 0.16 Hz
run 2: 0.153 Hz < 0.16 Hz
run 3: 0.16 Hz = 0.16 Hz
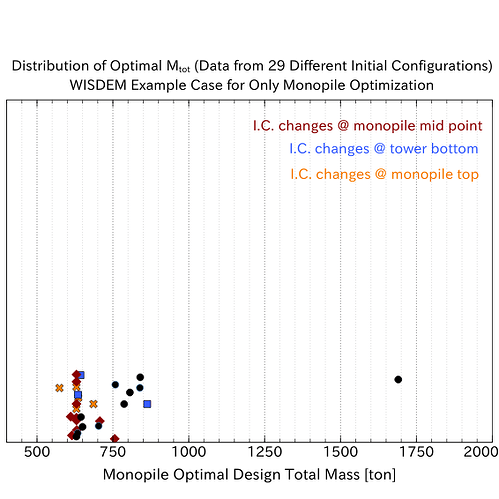
Summing up the values of tower mass and monopile mass found in the output file, the total structure masses are:
run 1: 3392 ton
run 2: 3350 ton
run 3: 3013 ton
So there is a difference in total mass values of about -1% between run 2 and run 1, and a difference of about -10% between run 3 and run 1.
The distributions of outer diameter and wall thickness of the optimal designs also change:

the diameter distributions differ of as much as about +1 m between run 2 and run 1 and between run 3 and run 1; the thickness distributions differ of as much as ~20 mm between run 2 and run 1 and between run 3 and run 1.

Now I am puzzled by the following questions:

1. I think that the difference in structural mass of about -1% between run 2 and run 1 is negligible, so I might consider those two optimizations to have output the same minimum for the structural mass. If so, why the diameter and thickness distributions of the optimal designs are not practically the same? If not so, can actually a difference of -0.3 m in the diameter at four points of the initial configuration of only the tower make a difference of as much as ~1 m along the optimal configuration of the tower and the monopile?

2. Can a difference in only the thickness of the initial configuration be responsible of differences in the outer diameter distributions of the optimal design?

3. Finally, how can the objective function structural mass for this relatively simple (correct me if I am wrong) optimization problem turn out to be multimodal, that is, to have different local minima instead of a single minimum?

I would really appreciate if someone could help me understand these results.

Thank you for your time and attention

[Garrett.Barter]

These are classic questions for optimization practitioners and often arise as one moves from theory to practice. Gradient-based optimization is heuristic, meaning it is path dependent and the path will change depending on initial conditions, algorithm settings, and convergence tolerance. With so many constraints, the regions of validity in the design space are not contiguous, so you are likely to find local minima. Additionally, with finite differences supplying the gradients, the gradients will be noisy and the algorithm won’t always proceed along the ideal path. Maybe you could overcome this by setting convergence tolerances that are tiny (~1e-10 or less), but then you would be waiting forever for convergence. These are all standard optimization issues and in no way unique to WISDEM or wind problems.

With all these challenges, a common practice in global optimization to improve rigor is “multistart” (which you can Google- apparently there is even a Matlab function for it). You essentially give many different initial conditions or settings, sometimes even dozens or hundreds of different ones, and either look for the best overall solution or look at trends among the results.