Dear Jason and others,
thanks for the quick advice. I comment on your points in the list below and explain some simulations I performed to get a little bit closer to the problem afterwards. At some points, I go pretty much into detail and I don’t expect anyone to take his or her time to go through all of this and follow my thoughts. Still, I would appreciate if you or anyone else likes to comment on certain parts.
- By “non-skewed wake” I mean that the skew angle of the wake should be equal to the yaw angle, which is not correct in reality but makes the discussion easier. Consequently, the influence of a wake skew correction should not be part of the discussion. Sorry for the misleading formulation.
- Thanks a lot for this hint. I tried to dig into the description of the UA model and comment on it below.
- I agree with you on the statement that in general variations of the AoA will have a significantly higher impact on the loads of a wind turbine than variations of the local inflow velocity. Nevertheless, this topic is of special interest for me, because I focus on the yaw moment wind turbines. (We already had a short discussion on this at the DEEPWIND this year, maybe you remember.) When neglecting the unsteady aerodynamics, the advancing and retarding blade effect is neutral in terms of its contribution to the mean yaw moment as the loads on the on the upwind and the downwind side are equal in average. The blade loads undergo a more or less sinosoidal variation, which reaches its maximum and minimum at 180° and 0° azimuth. When now considering a time lag effect on the blade loads, a small phase shift occurs, which shifts the maximum to one side of the rotor and the minimum to the other resulting in a non-zero mean yaw moment. Depending on the direction of this shift, the yaw moment will either be restoring or deflecting. Unfortunately, the time lag effect of the variation of the AoA on the blade loads causes a deflecting contribution (as the AoA decreases when passing from the downwind to the upwind side) while the time lag effect of the variation of the local inflow velocity causes a restoring contribution to the yaw moment (as the local inflow velocity increases when passing from the downwind to the upwind side). In general, I think it can be said that the circulation around the blade reaches its maximum when passing from the downwind to the upwind side, which means that the effect of the increasing inflow velocity is dominant here. I therefore expect the average yaw moment arising from the unsteady aerodynamics to be restoring, which would not be the case when only considering the time-lag effect of the AoA.
I digged a little bit into the equations from the description you posted, but surely did not get everything. From my point of view, all influences are summarized in the effective angle of incident:
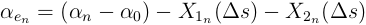
Where X_1n and X_2n are discrete exponential functions, which introduce the time lag:
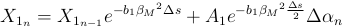
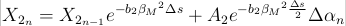
delta s is the distance that the airfoil traveled in the last time step non-dimensionalised with the half of the chord length. This distance is dependent on the relative inflow velocity. Therefore, - from my understanding - the local inflow velocity influences the time constant of the time lag.
My understanding of the derivation may be not completely correct, but when now considering a blade section with uniform, constant local inflow velocity and AoA, X1_n and X2_n should be zero. As delta alpha_n is also zero, this means that:
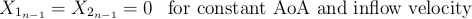
When now a sudden rise of the inflow velocity occurs (while the AoA stays constant), from my understanding only delta s changes while delta alpha_n as well as X_1(n-1) and X_2(n-1) are still zero. Therefore, both terms in the upper equations remain zero. This would mean that a variation of the local inflow velocity itslef would cause no time lag effect.
I would appreciate comments on this argumentation and hope that i didn’t miss anything fundamental.
- Thanks also for this hint. I did not use the stand alone driver until now, but it is surely easier to simulate some more distinct test simulations, when needed.
In order to check if the conclusions I draw from the argumentation in 3. may be correct, I tried to set up some simple test cases in OpenFAST with AeroDyn v15. This is surely not the cleanest way (in comparison to using the stand-alone driver) to do this, but I hope it works. The simulation is set-up as follows: Wind turbine rotor in parked Position (blade 1 at 0deg azimuth / pointing upwards), near 90° pitch angle to get a local AoA of around 2° at the blade section under observation, uniform inflow. WakeMod: none (no induction model). (Please ask, if information is missing.)
The first test case should model a sudden change of the AoA without any other effects. This is realised by a fast change of the inflow wind direction of 1deg. The graph below (and attached) shows the blade loads in y direction (which is more or less equal to the lift), the local AoA and the local inflow velocity of an exemplary blade section. The results without the Unsteady Aerodynamics model are represented in dashed lines.
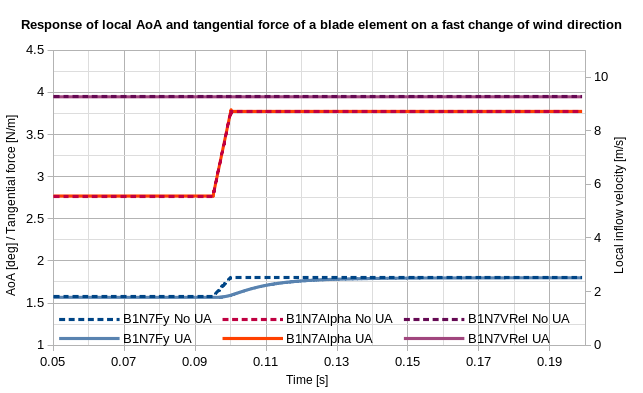
All in all, the graph shows the expected behaviour: A step-like increase of the AoA at constant local inflow velocity and a increase of the “lift” force. When using the UA model, a time lag is visible as response to the change of the AoA.
The second test case should model a sudden change of the local inflow velocity without any other effects. This is realised by a fast increase of the inflow wind velocity of 1 m/s. Results without UA are not plotted, as they are identical to the results with UA activated.

When looking at AoA and local inflow velocity, we can see a step-like increase of the inflow velocity while the AoA stays constant, which is the expected behaviour. The resulting “lift” force ideally follows the shape of the local inflow velocity without any time lag.
So from my tests, it seems that a change of the inflow velocity will have an influence on speed of the decay due to a change in the AoA. But a dynamic change of the local inflow velocity itself will not be captured by the UA model. Still, there may be some issues in the modeling or my understanding. I would appreciate some comments and would like to ask for some inconsistencies or possible mistakes in modeling you can see or guess.
Best regards and many thanks for the advice,
Christian



